Exercícios Resolvidos: Movimento Uniformemente Variado
Questões Resolvidas Sobre Movimento Uniformemente Variado
1. Testes realizados com o carro Gol mostraram que ele vai de 0 a 100 km/h em 10s. Calcule a aceleração aproximada do veículo nesse intervalo de tempo. (adote 100 km/h = 28 m/s)
a) 2,0 m/s²
b) 2,8 m/s²
c) 4,1 m/s²
d) 5,3 m/s²
e) 8,1 m/s²
2. Um automóvel que vinha a 25 m/s freou e parou em 25 s. O valor da aceleração escalar média do automóvel durante a freada foi de:
a) zero
b) -1,0 m/s²
c) 1,0 m/s²
d) -3,6 m/s²
e) 4,0 m/s²
3. Um avião a jato, partindo do repouso. é submetido a uma aceleração constante de 4 m/s². Qual o intervalo de tempo de aplicação desta aceleração para que o jato atinja a velocidade de decolagem de 160 m/s ?
a) 80s
b) 20s
c) 30s
d) 40s
e) 50s
4. A equação da velocidade de um móvel em movimento retilíneo é dada por v= 50 -4t, no sistema internacional. A velocidade desse móvel no instante 5 segundos é:
a) 50 m/s
b) 40 m/s
c) 30 m/s
d) 60 m/s
e) 70 m/s
5. Uma partícula se move ao longo do eixo x de modo que sua posição é descrita por x(t) = -10 + 2t + 3t², onde o tempo está em segundos e a posição, em metros. Calcule o módulo da velocidade média, em metros por segundo, no intervalo entre t = 1,0s e t = 2,0 s.
6. (Fuvest-SP) A velocidade máxima permitida em uma autoestrada é de 110 km/h (aproximadamente 30 m/s) e um carro, nessa velocidade, leva 6s para parar completamente. Diante de um posto rodoviário, os veículos devem trafegar no máximo a 36 km/h (10 m/s). Assim, para que os carros em velocidade máxima consigam obedecer ao limite permitido ao passar em frente do posto, a placa referente à redução de velocidade deverá ser colocada antes do posto a uma distância de, pelo menos:
a) 40 m.
b) 60 m.
c) 80 m.
d) 90 m.
e) 100 m.
b) zero
c) 2 m
d) 4 m
e) 8 m
7. (MACK-SP) Uma partícula em movimento retilíneo desloca-se de acordo com a equação v = -4 + t, onde v representa a velocidade escalar em m/s e t, o tempo em segundos, a partir do instante zero. O deslocamento dessa partícula no intervalo (0 s, 8 s) é:
a) 24 mb) zero
c) 2 m
d) 4 m
e) 8 m
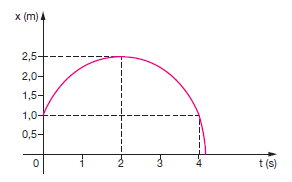
8. (Acafe-SC) O gráfico representa a variação da posição, em função do tempo, de um ponto material que se encontra em movimento retilíneo uniformemente variado.
Analisando o gráfico, podemos afirmar que:
a) A velocidade inicial é negativa.
b) A aceleração do ponto material é positiva.
c) O ponto material parte da origem das posições.
d) No instante 2 segundos, a velocidade do ponto material é nula.
e) No instante 4 segundos, o movimento do ponto material é progressivo.
9. (UFSC) Um carro está a 20 m de um sinal de tráfego quando este passa de verde a amarelo. Supondo que o motorista acione o freio imediatamente, aplicando ao carro uma desaceleração de 10 m/s², calcule, em km/h, a velocidade máxima que o carro pode ter, antes de frear, para que ele pare antes de cruzar o sinal.
10. Uma motocicleta se desloca com velocidade constante igual a 30m/s. Quando o motociclista vê uma pessoa atravessar a rua freia a moto até parar. Sabendo que a aceleração máxima para frear a moto tem módulo igual a 8m/s², e que a pessoa se encontra 50m distante da motocicleta. O motociclista conseguirá frear totalmente a motocicleta antes de alcançar a pessoa?
RESPOSTAS
Questão 1: [B]
v0 = 0
v = 100 km/h = 28 m/s
t = 10 s
v = v0 + a.t
28 = 0 + a . 10
10a = 28
a = 28/10
a = 2,8 m/s²
Questão 2: [B]
v0 = 25 m/s
v = 0
t = 25 s
v = v0 + a.t
0 = 25 + a . 25
25 + a . 25 = 0
25 + a . 25 = 0
25a = -25
a = -25/25
a = -1 m/s²
Questão 3: [D]
v0 = 0
v = 160 m/s
a = 4 m/s²
v = v0 + a.t
160 = 0 + 4.t
t = 160/4
t = 40 s
Questão 4: [C]
t = 5 s
v = 50 - 4.t
v = 50 - 4 . 5
v = 50 - 20
v = 30 m/s
Questão 5: [C]
Calculando as posições nos instantes mencionados:
x(t) = -10 + 2t + 3t²
x(1) = -10 + 2 (1) + 3 (1)² = -5 m
x(2) = -10 + 2 (2) + 3 (2)² = 6 m
vm = Δx/Δt
vm = 6 - (-5)/2 - 1
vm = 11 m/s
Questão 6: [C]
Considerando a aceleração escalar constante durante a freada do carro, temos:
v = v0 + at
0 = 30 + a . 6
a = -5m/s²
v² = v²0 + 2aΔs
10² = 30² + 2 (-5) Δs
Δs = 80 m
Questão 7: [B]
Temos:
v = -4 + t
Daí tiramos: v0 = -4 m/s e a = 1 m/s²
Aplicando em:
s = s0 + v0t + at²/2
Teremos:
s = 0 + (-4) . t + 1.t²/2
s = -4t + t²/2
Para t = 8 s, temos: s = -4(8) + 8²/2
s = -32 + 32
s = 0
Questão 8: [D]
Do gráfico temos:v0 > 0, a < 0, s0 = 1 m
Quando t = 2 s, v = 0 ( o ponto material muda de sentido)
Questão 9
Para essa questão, utilizaremos a fórmula de Torricelli: v² = v0² + 2aΔs
0 = v0² + 2(10).20
v0² = 400
v0 = 20m/s
Para transformar essa velocidade em km/h, basta multiplicar o valor encontrado em m/s por 3,6. Logo, a velocidade máxima que o carro pode ter é 72km/h.
Questão 10
A aceleração será negativa, pois ao frear a moto ela se opõe ao movimento.
v² = v0² + 2aΔs
0 = (30)² + 2 . (-8).Δs
-900 = -16Δs
Δs = 900/16
Δs = 56,25 m
Não conseguirá parar antes de atingir a pessoa.








ZOAS KKKKKKKKKKK